Stick and Ball Caves

Home --> Programming Projects --> Fractal Block Engine --> Procedural World Generation --> Stick And Ball Caves

The Idea

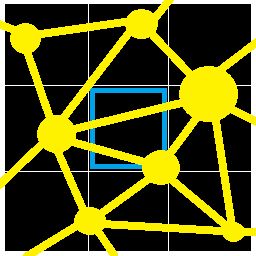
Please read this page about virtual chunks. For simplicity, we will assume on this page that each virtual chunk is the same size as the chunk being procedurally generated (the blue chunk in the picture).

Consider a model of a molecule what has balls connected together by sticks. This is what we mean by stick and ball caves. This is the primary cave generation technique in Fractal Block World.

For each of the 3x3x3 surrounding virtual chunks (surrounding the blue chunk being generated), we place balls. Each ball has a randomly generated radius. Then we iterate over all pairs of balls in the 3x3x3 region of virtual chunks. If two balls are less than the "max edge distance" apart, we join them with a stick.

Intersection Tests

Once we create all the balls and the sticks for the surrounding 3x3x3 region of chunks, we make a short list of all balls and sticks that intersect the blue chunk (the chunk being procedurally generated).

Note that it would be a mistake to make a list of all balls that intersect the blue chunk but then only consider sticks that connect those balls. There may be two balls that do not intersect the blue chunk, but the stick joining them DOES intersect the blue chunk.

First, we need a function that determines if a sphere intersects an axis aligned box. Here is Lua code for such a function:

--This is Lua code.
--Got from Ben Voigt's answer on stackoverlow.
--See: https://stackoverflow.com/questions/4578967/cube-sphere-intersection-test
--c1, c2 are the corners of the box.
--s is the center of the sphere.
--r is the radius of the sphere.
function box_intersects_sphere(c1, c2, s, r)
    local counter = r * r
    if      s.x < c1.x then counter = counter - p.squared(s.x - c1.x)
    elseif  s.x > c2.x then counter = counter - p.squared(s.x - c2.x) end
    if      s.y < c1.y then counter = counter - p.squared(s.y - c1.y)
    elseif  s.y > c2.y then counter = counter - p.squared(s.y - c2.y) end
    if      s.z < c1.z then counter = counter - p.squared(s.z - c1.z)
    elseif  s.z > c2.z then counter = counter - p.squared(s.z - c2.z) end
    return counter > 0
end

Determining if a stick intersects the blue chunk is more annoying. The key is the following function which determines if a line segment intersects an axis aligned box. Here is Lua code for such a function:

--This is Lua code.
--box_min, box_max are the corners of the box.
--seg_start and seg_end are the endpoints of the line segment.
--There is a less tedious way to write this code.
function seg_intersects_box(
    seg_start, seg_end,
    box_min, box_max)
--
    if( seg_start.x > box_max.x and
        seg_end.x   < box_max.x )
    then
        local param =
            (seg_start.x - box_max.x) /
            (seg_start.x - seg_end.x)
        local p_y = seg_start.y * (1.0 - param) + seg_end.y * param
        local p_z = seg_start.z * (1.0 - param) + seg_end.z * param
        if( p_y >= box_min.y and
            p_z >= box_min.z and
            p_y <= box_max.y and
            p_z <= box_max.z )
        then
            return true
        end
    end
    if( seg_start.y > box_max.y and
        seg_end.y   < box_max.y )
    then
        local param =
            (seg_start.y - box_max.y) /
            (seg_start.y - seg_end.y)
        local p_x = seg_start.x * (1.0 - param) + seg_end.x * param
        local p_z = seg_start.z * (1.0 - param) + seg_end.z * param
        if( p_x >= box_min.x and
            p_z >= box_min.z and
            p_x <= box_max.x and
            p_z <= box_max.z )
        then
            return true
        end
    end
    if( seg_start.z > box_max.z and
        seg_end.z   < box_max.z )
    then
        local param =
            (seg_start.z - box_max.z) /
            (seg_start.z - seg_end.z)
        local p_x = seg_start.x * (1.0 - param) + seg_end.x * param
        local p_y = seg_start.y * (1.0 - param) + seg_end.y * param
        if( p_x >= box_min.x and
            p_y >= box_min.y and
            p_x <= box_max.x and
            p_y <= box_max.y )
        then
            return true
        end
    end
    if( seg_start.x < box_min.x and
        seg_end.x   > box_min.x )
    then
        local param =
            (box_min.x - seg_start.x) /
            (seg_end.x - seg_start.x)
        local p_y = seg_start.y * (1.0 - param) + seg_end.y * param
        local p_z = seg_start.z * (1.0 - param) + seg_end.z * param
        if( p_y >= box_min.y and
            p_z >= box_min.z and
            p_y <= box_max.y and
            p_z <= box_max.z )
        then
            return true
        end
    end
    if( seg_start.y < box_min.y and
        seg_end.y   > box_min.y )
    then
        local param =
            (box_min.y - seg_start.y) /
            (seg_end.y - seg_start.y)
        local p_x = seg_start.x * (1.0 - param) + seg_end.x * param
        local p_z = seg_start.z * (1.0 - param) + seg_end.z * param
        if( p_x >= box_min.x and
            p_z >= box_min.z and
            p_x <= box_max.x and
            p_z <= box_max.z )
        then
            return true
        end
    end
    if( seg_start.z < box_min.z and
        seg_end.z   > box_min.z )
    then
        local param =
            (box_min.z - seg_start.z) /
            (seg_end.z - seg_start.z)
        local p_x = seg_start.x * (1.0 - param) + seg_end.x * param
        local p_y = seg_start.y * (1.0 - param) + seg_end.y * param
        if( p_x >= box_min.x and
            p_y >= box_min.y and
            p_x <= box_max.x and
            p_y <= box_max.y )
        then
            return true
        end
    end
    if( seg_start.x >= box_min.x and
        seg_start.y >= box_min.y and
        seg_start.z >= box_min.z and
        seg_start.x <= box_max.x and
        seg_start.y <= box_max.y and
        seg_start.z <= box_max.z )
    then
        --seg_start is inside box.
        return true
    end
    return false
end

Then to determine if a cylinder (surrounding a line segment) intersects a box, we simply extrude the box by the radius of the cylinder and then intersect the line segment with the extruded box. This does not make 100% complete sense, but it is close enough.

--This is Lua code.
--box_min and box_max are the corners of the box.
--seg_start and seg_ends are the endpoints of the line segment.
--radius is the radius of the cylinder surrounding the line segment.
function box_intersects_cylinder(
    box_min, box_max,
    seg_start, seg_end, radius)
--
    local ext_box_min = vec(
        box_min.x-radius,
        box_min.y-radius,
        box_min.z-radius)
    local ext_box_min = vec(
        box_max.x+radius,
        box_max.y+radius,
        box_max.z+radius)
    return seg_intersects_box(
        seg_start, seg_end, ext_box_min, ext_box_max)
end

Iterating Over all Block Positions

Once we have our short list of all balls and sticks that intersect the blue chunk (the chunk being generated), we then must iterate over every block position in the blue chunk and see if the block position is close enough to either a ball or a stick.

This is relatively slow because there are 16x16x16 block positions in a chunk.

Determining if a block position is close enough to a sphere is easy: we compute the square of the distance from the center of the block position to the center of the ball. We then compare that with the square of the radius of the ball. Doing it this way, we do not have to compute any square roots.

Determining if a block position is close enough to a stick is more annoying. We use the following (Lua) code:

--This is Lua code.
--p is the point.
--v1,v2 are the endpoints of the line segment.
--r is the radius of the cylinder that surrounding the line segment.
function vec_close_to_cylinder(p, v1, v2, r)
    local a = vec_sub(v2,v1)  --v2 minus v1
    local b = vec_sub(p,v1)   --p minus v1
    local u = proj_of_b_on_a(a,b) --Standard vector projection.
    local dot = dot(u,a)
    if dot < 0.0 then return false end
    if dot > dot(a,a) then return false end
    local dist_sq = length_sq(vec_sub(u,b))
    return dist_sq < r*r
end

This code can be optimized. For example, when we compute the projection of b onto a, we must divide by a dot a. We could cache a, a dot a, and 1 divided by a dot a and use these values for all 16x16x16 block positions.

Maximum Radius of a Ball

For a technical reason, the maximum radius of a sphere is 16 blocks (this is because a chunk is 16 blocks wide). If we had a sphere with a larger radius, it might spill over into a chunk that is 2 chunks away, which would require us to consider the 5x5x5 virtual chunks surrounding the chunk being generated (which we do not want to do).

Maximum Stick Length

Just like the case with balls, the maximum stick length is 16 blocks (because a chunk is 16 blocks wide).

Varying the Maximum Stick Length per Chunk

If you want, you could have each chunk specify its own maximum stick length (which is at most 16).

With the simple implementation of this, there could be balls in adjacent chunks, and a stick that goes from out of one but not the other. See this picture:

We think it is probably best to just not worry about this. However one fix would be to iterate over all chunks intersecting a stick and take the maximum of the max stick length of all those chunks. This seems like a lot of work. Note that taking the max of the max stick lengths over all 3x3x3 chunks would also yield similar bad artifacts.

Modifying Stick and Ball Data by a Chunk's Block Type

We can make it so the stick and balls given by a chunk depend on that chunk's block type. This is safe because the procedural world generation system has access to the block types of all chunks in the 3x3x3 region surrounding the chunk being generated (see here).

Here is a picture showing adjacent chunks that have different block types but which are using a continuously changing stick and ball system.

Actually in this picture we are using virtual chunks that are each 2x2x2 normal chunks. This allows us to have sticks with length at most 2 * 16 = 32.

Level of Detail (LOD)

Here is a picture showing stick and balls with two levels of detail. Since we are close enough to a huge stick and at the same time we are small, the stick looks like a huge cylinder.

Stick and Ball Caves in Fractal Block World

The following are some pictures of stick and ball caves in fractal block world.

Here we are subtracting stick and balls from a solid area to create caves. This is why we call them "stick and ball caves".

Here is a similar picture. We are in the middle of a carved out ball, and from this position we can see the center of several other carved out balls. We can fly between the carved out balls by going through the caved out sticks.

Perlin Noise vs Stick and Balls?

Is it better to make caves using Perlin noise or with Sticks and Balls? We do not have an ultimate answer here, but one could easily incorporate both methods into a game. They are not mutually exclusive. Also, the techniques give different results.

Note that one must be careful when using the stick and ball method to not make it very slow. Part of the problem is there can be several balls/sticks intersecting the chunk being generated. On the other hand, the Perlin noise method is easier to make fast.